Skirtingai, standartinis nuokrypis yra skaičiuojant dispersiją gauta skaitinė vertė. Daugelis žmonių kontrastuoja šias dvi matematines sąvokas. Taigi, šiame straipsnyje bandoma atskleisti svarbų skirtumą tarp dispersijos ir standartinio nuokrypio.
Palyginimo diagrama
| Palyginimo pagrindas | Skirtumas | Standartinis nuokrypis |
|---|---|---|
| Reikšmė | Variancija - tai skaitinė vertė, kuri apibūdina stebimų skirtumą nuo jo aritmetinio vidurkio. | Standartinis nuokrypis - tai pastabų, esančių duomenų rinkinyje, sklaidos matas. |
| Kas tai? | Tai yra kvadratinių nuokrypių vidurkis. | Tai yra vidutinis kvadratinis nuokrypis. |
| Pažymėta kaip | Sigma-kvadratas (σ ^ 2) | Sigma (σ) |
| Išreikštas | Kvadratiniai vienetai | Tie patys vienetai, kaip ir duomenų rinkinio vertės. |
| Rodo | Kiek žmonių yra grupėje. | Kiek duomenų rinkinio pastabų skiriasi nuo jos vidurkio. |
Variancijos apibrėžtis
Statistikoje dispersija apibrėžiama kaip kintamumo matas, kuris parodo, kiek grupės nariai yra paskirstyti. Ji nustato vidutinį laipsnį, kuriuo kiekvienas stebėjimas skiriasi nuo vidurkio. Kai duomenų rinkinio dispersija yra nedidelė, tai rodo, kad duomenys yra artimi vidurkiui, o didesnė dispersijos vertė rodo, kad stebėjimai yra labai išsklaidyti aplink aritmetinį vidurkį ir vienas nuo kito.
Neslaptiems duomenims :
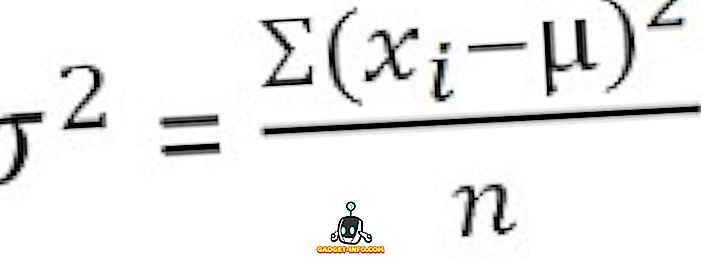
Grupiniam dažnių paskirstymui :
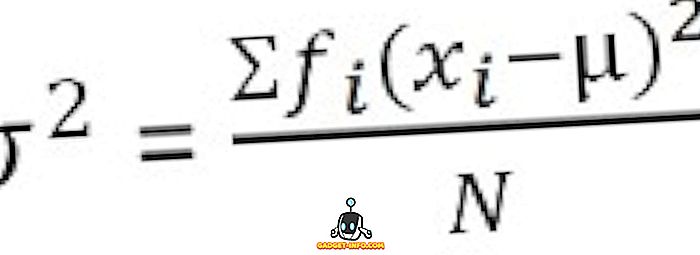
Standartinis nuokrypio apibrėžimas
Standartinis nuokrypis yra matas, kuriame kiekybiškai įvertinama duomenų rinkinyje esančių pastabų sklaida. Mažas standartinis nuokrypis yra taškų artumo su aritmetiniu vidurkiu ir dideliu standartiniu nuokrypiu rodiklis; balai yra išsklaidyti aukštesnėje reikšmių grupėje.
Neslaptiems duomenims :

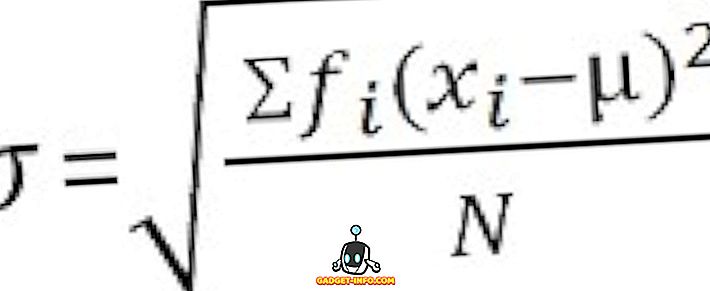
Pagrindiniai skirtumai tarp dispersijos ir standartinio nuokrypio
Skirtumas tarp standartinio nuokrypio ir dispersijos gali būti aiškiai matomas dėl šių priežasčių:
- Variancija - tai skaitinė vertė, kuri apibūdina stebimų skirtumą nuo jo aritmetinio vidurkio. Standartinis nuokrypis - tai pastabų, esančių duomenų rinkinyje, sklaidos matas.
- Skirtumas yra tik vidutinis kvadratinių nuokrypių skaičius. Kita vertus, standartinis nuokrypis yra vidutinis kvadratinis nuokrypis.
- Variancija žymima sigma kvadratu (σ2), o standartinis nuokrypis yra pažymėtas kaip sigma (σ).
- Skirtumas yra išreiškiamas kvadratiniais vienetais, kurie paprastai yra didesni už nurodytas duomenų rinkinio vertes. Priešingai nei standartinis nuokrypis, išreikštas tomis pačiomis dalimis, kaip ir duomenų rinkinio vertės.
- Variancija matuoja, kiek žmonių yra grupėje. Priešingai, standartinis nuokrypis matuoja, kiek duomenų rinkinio stebėjimai skiriasi nuo vidurkio.
Iliustracija
Žymiai, kuriuos studentas įvertino penkiuose dalykuose, yra atitinkamai 60, 75, 46, 58 ir 80. Turite sužinoti standartinį nuokrypį ir dispersiją.
Visų pirma, turite išsiaiškinti vidurkį,

Taigi vidutinis (vidutinis) ženklas yra 63, 8
Dabar apskaičiuokite dispersiją
| X | A | (xA) | (XA) ^ 2 |
|---|---|---|---|
| 60 | 63.8 | -3, 8 | 14.44 |
| 75 | 63.8 | 11.2 | 125.44 |
| 46 | 63.8 | -17, 8 | 316, 84 |
| 58 | 63.8 | 5.8 | 33.64 |
| 80 | 63.8 | 16.2 | 262, 44 |
Kur, X = Pastabos
A = aritmetinis vidurkis
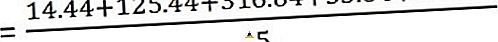
Ir standartinis nuokrypis yra -

Panašumai
- Ir dispersijos, ir standartiniai nuokrypiai visada yra teigiami.
- Jei visi duomenų rinkinyje esantys stebėjimai yra identiški, standartinis nuokrypis ir dispersija bus lygūs nuliui.
Išvada
Šie du yra pagrindiniai statistiniai terminai, kurie vaidina svarbų vaidmenį įvairiuose sektoriuose. Pageidautina, kad standartinis nuokrypis būtų didesnis už vidutinį, nes jis išreiškiamas tomis pačiomis dalimis kaip matavimai, o dispersija yra išreikšta vienetais, didesniais už nurodytą duomenų rinkinį.