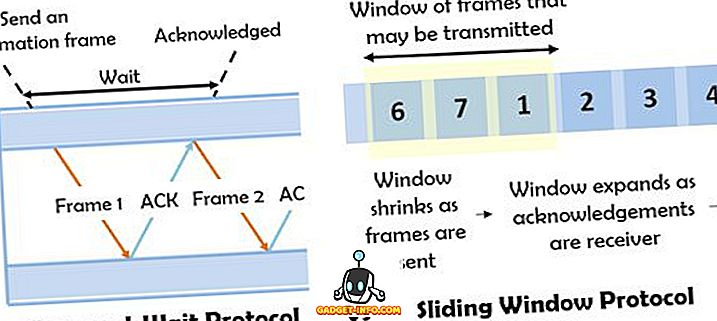
Priešingai, derinio atveju pavedimas visiškai nesvarbus. Ne tik matematikoje, bet ir praktiniame gyvenime mes reguliariai einame per šias dvi koncepcijas. Nors tai niekada nepastebime. Taigi, atidžiai perskaitykite straipsnį, kad sužinotumėte, kaip šios dvi sąvokos skiriasi.
Palyginimo diagrama
| Palyginimo pagrindas | Permutacija | Derinys |
|---|---|---|
| Reikšmė | Permutacija reiškia įvairius būdus, kaip suskirstyti objektų rinkinį eilės tvarka. | Kombinacija reiškia kelis būdus, kaip pasirinkti daiktus iš didelių objektų rinkinio, kad jų tvarka nesvarbi. |
| Įsakymas | Aktualus | Nesvarbus |
| Žymi | Išdėstymas | Pasirinkimas |
| Kas tai? | Užsakyti elementai | Nereguliuojami rinkiniai |
| Atsakymai | Kiek skirtingų išdėstymų galima sukurti iš tam tikrų objektų rinkinio? | Kiek skirtingų grupių galima pasirinkti iš didesnės objektų grupės? |
| Išvestinė | Daugkartinė permutacija iš vieno derinio. | Vienas derinys iš vieno permutacijos. |
Permutacijos apibrėžimas
Permutaciją apibrėžiame kaip įvairius būdus, kaip kai kuriuos ar visus rinkinio narius susitarti tam tikra tvarka. Tai reiškia, kad visi galimi duotojo rinkinio išdėstymai ar pertvarkymai skiriasi į atskirą tvarką.
Pavyzdžiui, visos galimos permutacijos, sukurtos raidėmis x, y, z -
- Vienu metu imant visus tris, yra xyz, xzy, yxz, yzx, zxy, zyx.
- Atsižvelgiant du vienu metu yra xy, xz, yx, yz, zx, zy.
Bendras galimų n dalykų permutacijų skaičius, paimtas r vienu metu, gali būti apskaičiuojamas taip:
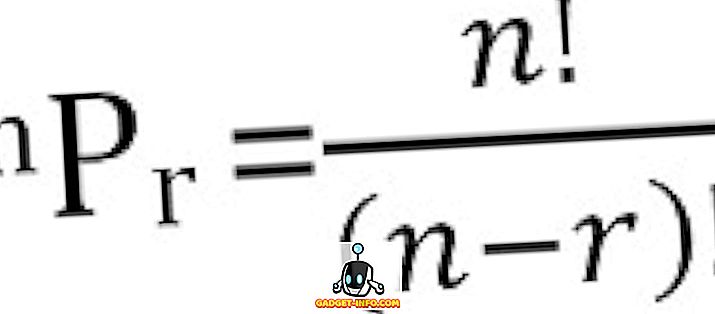
Kombinacijos apibrėžimas
Derinys apibrėžiamas kaip skirtingi būdai, kaip pasirinkti grupę, atsižvelgiant į kai kuriuos ar visus rinkinio narius, be šios tvarkos.
Pavyzdžiui, visi galimi deriniai, pasirinkti su raide m, n, o -
- Pasirenkant tris iš trijų raidžių, vienintelis derinys yra mno
- Pasirinkus dvi iš trijų raidžių, galimi deriniai yra mn, ne, om.
Bendras galimų n dalykų derinių, paimtų r vienu metu, skaičius gali būti apskaičiuojamas taip:
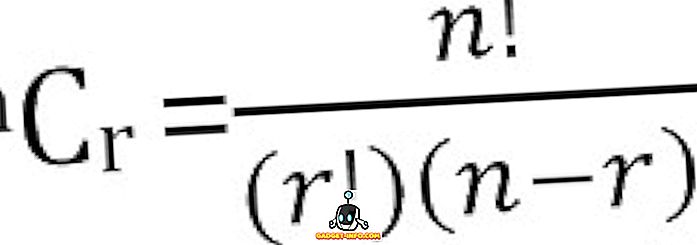
Pagrindiniai atotrūkio ir kombinacijos skirtumai
Skirtumai tarp permutacijos ir derinio aiškiai nurodomi dėl šių priežasčių:
- Terminas „permutacija“ reiškia kelis būdus, kaip surinkti objektų rinkinį nuoseklioje eilėje. Kombinacija reiškia kelis būdus, kaip pasirinkti daiktus iš didelio objektų grupės, todėl jų tvarka yra nesvarbi.
- Pagrindinis šių dviejų matematinių sąvokų skiriamasis bruožas yra tvarka, vieta ir pozicija, ty minėtose permutacinėse charakteristikose yra reikšmė, kuri nėra svarbi derinio atveju.
- Permutacija reiškia kelis būdus, kaip tvarkyti daiktus, žmones, skaitmenis, abėcėlę, spalvas ir tt Kita vertus, derinys nurodo įvairius meniu elementų, maisto, drabužių, dalykų ir pan. Pasirinkimo būdus.
- Permutacija yra tik užsakytas derinys, o kombinacija reiškia, kad tam tikruose kriterijuose yra netvarkingi rinkiniai arba vertybių poravimas.
- Daugelį permutacijų galima gauti iš vieno derinio. Priešingai, iš vieno permutacijos galima gauti tik vieną kombinaciją.
- Atsakymo atsakymai Kiek skirtingų priemonių galima sukurti iš tam tikrų objektų rinkinio? Priešingai nei derinys, paaiškinantis, kiek skirtingų grupių galima pasirinkti iš didesnės objektų grupės?
Pavyzdys
Tarkime, yra situacija, kai turite išsiaiškinti, kiek iš visų dviejų A, B, C objektų galima paimti du pavyzdžius. Šiame klausime, pirmiausia, reikia suprasti, ar klausimas susijęs su permutacija arba vienintelis būdas tai išsiaiškinti yra patikrinti, ar užsakymas yra svarbus, ar ne.
Jei užsakymas yra reikšmingas, klausimas yra susijęs su permutacija, o galimi mėginiai bus AB, BA, BC, CB, AC, CA. Kur, AB skiriasi nuo BA, BC skiriasi nuo CB ir AC yra skirtingas CA.
Jei užsakymas yra nesvarbus, klausimas yra susijęs su deriniu, o galimi mėginiai bus AB, BC ir CA.
Išvada
Atsižvelgiant į pirmiau minėtą diskusiją, aišku, kad permutacija ir derinys yra skirtingi terminai, naudojami matematikoje, statistikoje, tyrimuose ir mūsų kasdieniame gyvenime. Reikėtų prisiminti, kad dėl šių dviejų sąvokų tam tikram objektų rinkiniui permutacija visada bus didesnė už jos derinį.